Joshua Bengio published a couple of years ago a very interesting paper on representation learning. The paper is entitled “Representation Learning: A Review and New Perspectives“.
In this article he does an excellent job of describing the various priors that are used in representation learning. It’s a well established fact of machine learning that it is impossible to learn something without a prior. Note that I am not using here the word prior in the Bayesian sense. In this context I am referring to any kind of assumption that an algorithm makes regarding the structure of the problem. Another similar (but not equivalent) way to describe this would be the inductive bias of an algorithm.
I will write a short description here of some of the priors discussed on the paper and how they relate to commonly used algorithms.

The most common type of bias in machine learning is that of smoothness. This means that the function to be learned f is s.t. x ≈ y generally implies f(x) ≈ f(y). This roughly translates as “similar inputs should provide similar outputs”. Obviously, this is a reasonable assumption to make for lots of problems but also wrong for any situation where non-linearities are involved. This prior is first and foremost used in linear regression or any other similar method, such as the generalized linear model. This assumption can be relaxed in these methods with the introduction of non-linear terms (such as the square or the logarithm of a feature). This assumption is also quite strong in k-nearest neighbours.
Another type of prior that is commonly used is that of the hierarchical organisation of the explanatory factors. This is the primary assumption in models such as factor analysis or multilevel models. It is also one reason that deep neural nets have had so much success in visual and acoustic tasks, since the structure of these tasks is inherently hierarchical. Actually, our visual cortex is designed in a hierarchical function, as well.
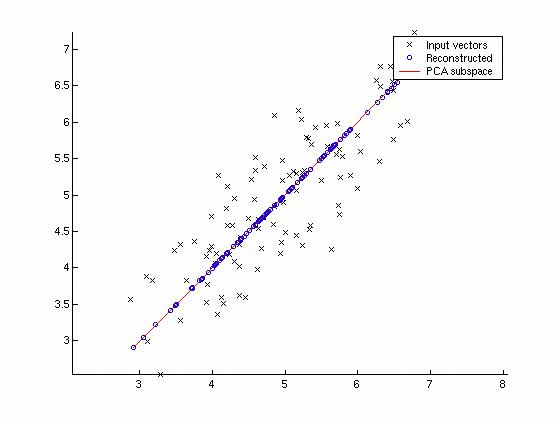
Factor analysis is also involved in another prior, that of manifolds. According to this prior, the real space we are operating in has a lower dimensionality that the one suggested by the number of variables. The most common method for this type of problems is Principal Component Analysis. In the figure below you see an example of a dataset with two variables, where the true dimensionality of the problem is equal to 1. Even though there are two variables the data can be described quite well by moving alongside a single component. In that particular case, it might be advantageous to use this component in a supervised model, instead of the two original variables.
Another common prior is that of clustering. Quite often the data falls within distinct clusters, so by discovering and labelling them, we improve the performance of a supervised model. Clustering is quite close to how the human brain operates, since language and society separates entities into discrete categories (e.g. animals, plants, humans). A lot of machine learning is actually reverse-engineering this process.
Sparsity is another prior that has become common in the last decade or so. According to this, given a large number of variables only a handful of them are useful for a particular problem. This prior is utilised by the LASSO and the elastic net algorithms. Sparsity is pretty common in recommender systems, since for a given website (say an online retailer like Amazon) the majority of users will not have purchased the majority of items. So, there are only a few data points to describe a single user. Especially, for big retailers, the majority of the users will not have interacted with more than 99% of the items available, either through buying or browsing the website.
It is always useful to think about the prior of a particular algorithm and the problem at hand, since this can only lead to a better choice of methods for a problem. Also, quite often, we can get insight into a problem but observing which methods work and which do not and what their associated assumptions are.

